传送带模型分析

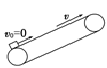
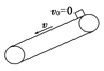
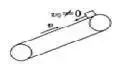
情景	传送带类别	图示	滑块可能的运动情况	滑块受（摩擦）力分析
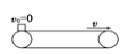
情景1	水平		一直加速	受力f=μmg
			先加速后匀速	先受力f=μmg，后f=0
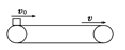
情景2	水平		v0>v，一直减速	受力f=μmg
			v0>v，先减速再匀速	先受力f=μmg，后f=0
			v0<v，一直加速	受力f=μmg
			v0<v，先加速再匀速	先受力f=μmg，后f=0
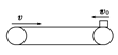
情景3	水平		传送带长度l<，滑块一直减速到达左端	受力f=μmg（方向一直向右）
			传送带长度l≥，v0<v，滑块先减速再向右加速，到达右端速度为v0	受力f=μmg（方向一直向右）
			传送带长度l≥，v0>v，滑块先减速再向右加速，最后匀速，到达右端速度为v	减速和反向加速时受力f=μmg（方向一直向右），匀速运动f=0
情景4	倾斜		一直加速	受摩擦力f=μmgcosθ
			先加速后匀速	先受摩擦力f=μmgcosθ，后f=mgsinθ
情景5	倾斜		一直加速	受摩擦力f=μmgcosθ
			先加速后匀速	先受摩擦力f=μmgcosθ，后f=mgsinθ
			先以加速度a1加速，后以加速度a2加速	先受摩擦力f=μmgcosθ，后受反向的摩擦力f=μmgcosθ
情景6	倾斜		一直加速	受摩擦力f=μmgcosθ
			先加速后匀速	先受摩擦力f=μmgcosθ，后f=mgsinθ
			一直匀速（v0>v）	受摩擦力f=mgsinθ
			一直匀速（v0=v）	受摩擦力f=0
			先以加速度a1加速，后以加速度a2加速	先受摩擦力f=μmgcosθ，后受反向的摩擦力f=μmgcosθ
情景7	倾斜		一直加速	受摩擦力f=μmgcosθ
			一直匀速	受摩擦力f=mgsinθ
			先减速后反向加速	受摩擦力f=μmgcosθ，

应用举例

【例1】如图1所示，一水平传送装置由轮半径均为R的主动轮O₁和从动轮O₂及传送带等构成。两轮轴心相距8.0 m，轮与传送带不打滑。现用此装置运送一袋面粉，已知这袋面粉与传送带之间的动摩擦因数为μ＝0.4。（g取10 m/s2）求

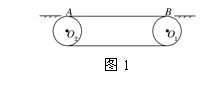
（1）当传送带以4.0 m/s的速度匀速运动时，将这袋面粉由左端O₂正上方的A点轻放在传送带上后（设面粉初速度近似为零），这袋面粉由A端运送到O₁正上方的B端所用的时间为多少？

（2）要想尽快将面粉由A端送到B端，主动轮O1的转速至少应为多大？

【解析】设这袋面粉质量为m，其在与传送带产生相对滑动的过程中所受摩擦力f＝μmg。故其加速度为a＝＝μg＝4.0 m/s²。

（1）若传送带的速度v带＝4.0 m/s，则这袋面粉加速运动的时间t1＝v带/a＝1.0 s，在t₁时间内的位移x1为x1＝at₁²＝2.0 m。

其后以v＝4.0 m/s的速度做匀速运动，

x₂＝l_AB－x₁＝vt₂，

解得：t₂＝1.5 s。

运动的总时间为：t＝t₁＋t₂＝2.5 s。

（2）要想时间最短，这袋面粉应一直向B端做加速运动，由lAB＝at′2可得t′＝2.0 s。

面粉到达B端时的速度v′＝at′＝8.0 m/s，即传送带运转的最小速度。

由v′＝ωR＝2πnR可得：n=？r/min。

【例2】如图2所示，质量为m的物体从离传送带高为H处沿光滑圆弧轨道下滑，水平滑上长为L的静止的传送带并落在水平地面的Q点，已知物体与传送带间的动摩擦因数为μ，则当传送带转动时，物体仍以上述方式滑下，将落在Q点的左边还是右边 ？

【解析】物体从P点滑下，设水平滑上传送带时的速度为v0，则由机械能守恒mgH=mv02，可得。

当传送带静止时，分析物体在传送带上的受力知物体做匀减速运动，a=μmg/m=μg。物体离开传送带时的速度为，随后做平抛运动而落在Q点。当传送带逆时针方向转动时，分析物体在传送带上的受力情况与传送带静止时相同，因而物体离开传送带时的速度仍为，随后做平抛运动而仍落在Q点。（当v02<2μgL时，物体将不能滑出传送带而被传送带送回，显然不符合题意）

当传送带顺时针转动时，可能出现五种情况：

（1）当传送带的速度v较小，时，分析物体在传送带上的受力可知，物体一直做匀减速运动，离开传送带时的速度为，因而仍将落在Q点。

（2）当传送带的速度时，分析物体在传送带上的受力可知，物体将在传送带上先做匀减速运动，后做匀速运动，离开传送带时的速度，因而将落在Q点的右边。

（3）当传送带的速度=v0时，则物体在传送带上不受摩擦力的作用而做匀速运动，离开传送带时的速度，因而将落在Q点的右边。

（4）当传送带的速度时，分析物体在传送带上的受力可知，物体将在传送带上先做匀加速运动，后做匀速运动，离开传送带时的速度，因而将落在Q点的右边。

（5）当传送带的速度v较大 时，分析物体在传送带上的受力可知，物体一直做匀加速运动，离开传送带时的速度为，因而将落在Q点的右边。

综上所述：

当传送带逆时针转动或顺时针转动且速度时，物体仍将落在Q点；

当传送带顺时针转动且速度时，物体将落在Q点的右边。

【例3】如图3所示，绷紧的传送带，始终以2 m/s的速度匀速斜向上运行，传送带与水平方向间的夹角θ＝30°。现把质量为10 kg的工件轻轻地放在传送带底端P处，由传送带传送至顶端Q处。已知P、Q之间的距离为4 m，工件与传送带间的动摩擦因数为μ＝，取g＝10 m/s2。求：

 

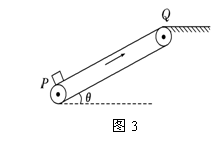
（1）通过计算说明工件在传送带上做什么运动；

（2）求工件从P点运动到Q点所用的时间。

【解析】（1）对工件进行受力分析，由牛顿第二定律得：

μmgcosθ－mgsinθ＝ma，

代入数值得：a＝2.5 m/s²。

则其速度达到传送带速度时发生的位移为x1＝＝0.8 m<4 m。

可见工件先匀加速运动0.8 m，然后匀速运动3.2 m。

（2）匀加速时，由x1＝t1得t1＝0.8 s，

匀速上升时t2＝＝1.6 s，

所以工件从P点运动到Q点所用的时间为t＝t1＋t2＝2.4 s。

【例4】如图4所示，传送带与水平面夹角为37°，并以v=10m/s运行，在传送带的A端轻轻放一个小物体，物体与传送带之间的动摩擦因数μ=0.5，AB长16 m，求：以下两种情况下物体从A到B所用的时间。

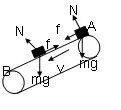
（1）传送带顺时针方向转动；

（2）传送带逆时针方向转动。

【解析】（1）传送带顺时针方向转动时受力如图4-1，由牛顿第二定律得

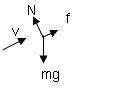
mgsinθ－μmgcosθ=ma，

物体下滑的加速度为a=gsinθ－μgcosθ=2m/s2。

加速的位移为s=at2，故有加速的时间为：。

（2）传送带逆时针方向转动物体受力如图4-2，开始摩擦力方向向下，向下匀加速运动。

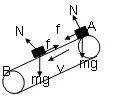
a=gsin37°+μgcos37°=10m/s²，

加速的时间为t1=v/a=1s。

加速的位移为s1=at2 =5m，

还剩位移s2=11m。

由题意，1s后，速度达到10m/s，摩擦力方向变为向上，由牛顿第二定律得

a2=g sin37°-μg cos37°=2 m/s²。

由运动学公式得s₂=vt²+a2t₂²，解得t₂=1s，

故从A点到B点的时间为t=t₁+t₂=2s。

题后反思

在水平方向的传送带问题中物块的受力主要是讨论滑动摩擦力，在存在相对运动时就会存在摩擦力，因此分析问题时以滑块是否与传送带共速为临界进行分析讨论。

在斜面方向上的传送带问题中物块的受力就要复杂些了，物体相对传送带滑动或者有滑动的趋势是判断摩擦力方向的关键，比如滑块受到沿斜面向下的滑动摩擦力作用，这样物体在沿斜面方向上所受的合力为重力的下滑分力和向下的滑动摩擦力，物体要做匀加速运动。当物体加速到与传送带有相同速度时，摩擦力情况要发生变化，同速的瞬间可以看成二者间相对静止，无滑动摩擦力，但物体此时还受到重力的下滑分力作用，因此相对于传送带有向下的运动趋势。若重力的下滑分力大于物体和传送带之间的最大静摩擦力，此时有μ＜tanθ，则物体将向下加速，所受摩擦力为沿斜面向上的滑动摩擦力；若重力的下滑分力小于或等于物体和传送带之间的最大静摩擦力，此时有μ≥tanθ，则物体将和传送带相对静止一起向下匀速运动，所受静摩擦力沿斜面向上，大小等于重力的下滑分力。也可能出现的情况是传送带比较短，物体还没有加速到与传送带同速就已经滑到了底端，这样物体全过程都是受沿斜面向上的滑动摩擦力作用。