内切球半径公式

初中所学习的三角形内切圆半径公式,其推导过程是利用等面积法。
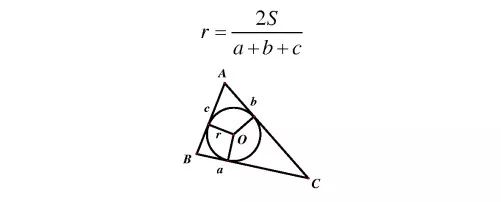
类比等面积法我们容易联想到等体积法,既而推导出三棱锥的内切球半径公式:
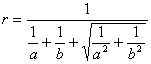
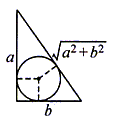
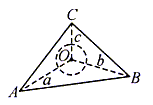
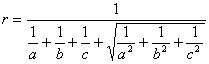 。
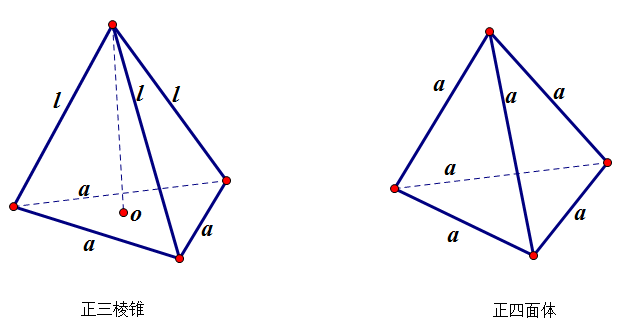
。

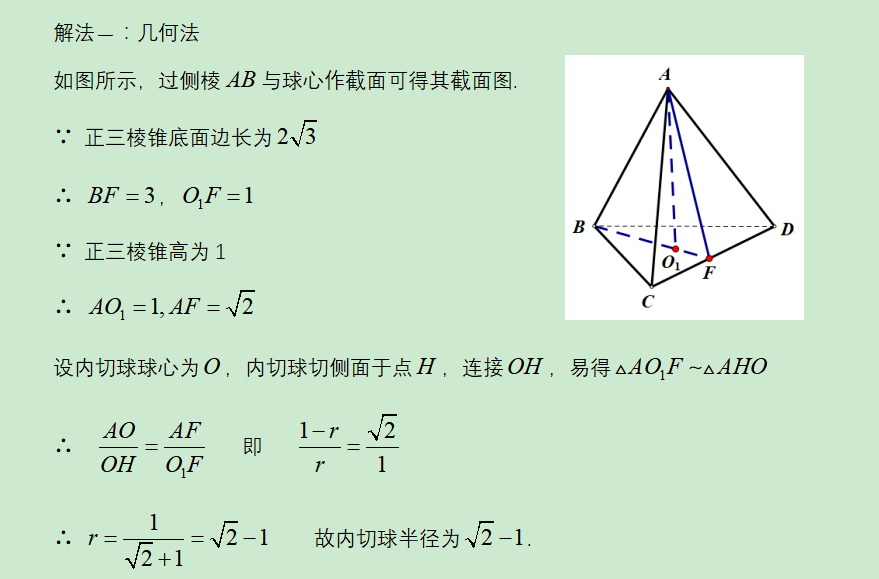
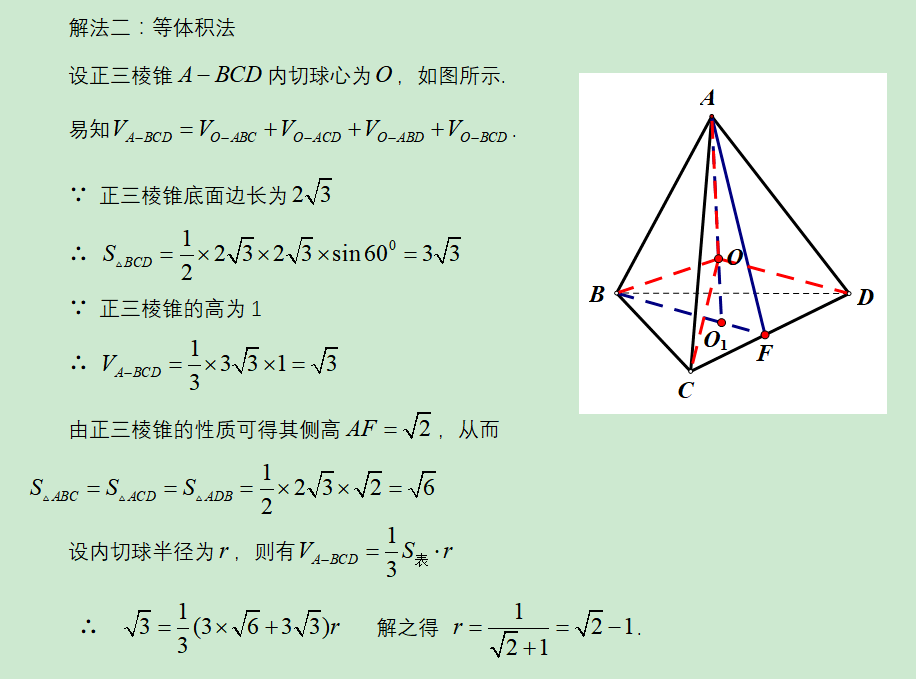
浏览次数:
发布日期:
2024-10-28 18:26:24
内切球半径公式

初中所学习的三角形内切圆半径公式,其推导过程是利用等面积法。
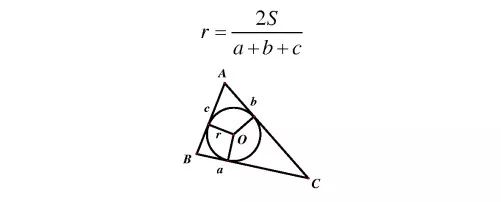
类比等面积法我们容易联想到等体积法,既而推导出三棱锥的内切球半径公式:
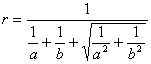
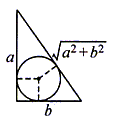

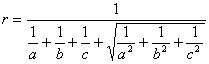 。
。


